소수(prime number)는 1과 자기 자신만을 약수로 가지는 수이다.
프로그래머스나 백준 등 다양한 알고리즘 문제에서, "1부터 N까지의 소수를 모두 구하라"는 문제는 자주 등장한다.
이때, 가장 효율적으로 소수를 구하는 고전 알고리즘이 바로 **에라토스테네스의 체 (Sieve of Eratosthenes)**이다.

에라토스테네스의 체란?

에라토스테네스의 체는 다음과 같은 방식으로 동작한다:

1. 2부터 N까지 모든 정수를 나열한다.
1. 현재 수를 소수로 판단하고, 그 수의 배수들을 모두 제거한다.
1. 남은 수들 중 다음으로 작은 수를 반복해서 소수로 판단한다.
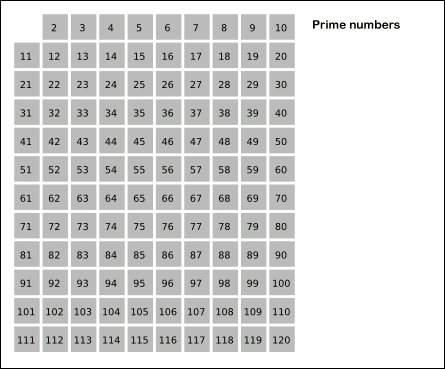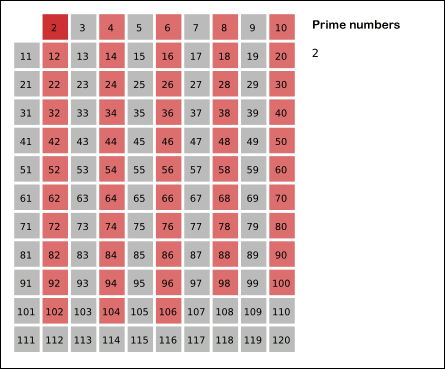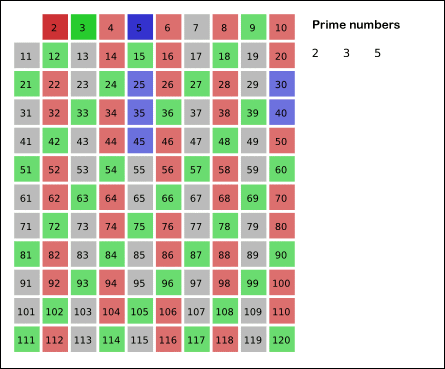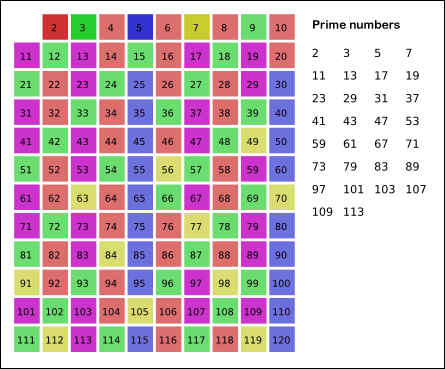
1. N까지 반복한다.

결과적으로 제거되지 않은 수들만 소수로 남는다.

에라토스테네스의 체 구현하기 - JavaScript

소수 알고리즘 문제와 함께 JavaScript로 구현한 이 알고리즘을 코드와 함께 정확하게 알아보자.

문제 설명
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.

소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)

제한 조건
n은 2이상 1000000이하의 자연수입니다.


입출력 예
n	result
---------
10	4
5	3

시간 복잡도 실패한 초기 코드

function solution(n) {
  var answer = 0;
 
  for (let i = 2; i <= n; i++) {
    if (prime(i)) answer++;
  }
 
  return answer;
}
 
function prime(n) {
  for (let i = 2; i < n; i++) {
    if (n % i === 0) {
      return false;
    }
  }
 
  return true;
}

위 코드는 소수를 판별하는 prime 함수를 사용하여 2부터 n까지의 모든 수를 검사한다.
이 방식은 시간 복잡도가 O(n^2)으로, n이 커질수록 성능이 급격히 저하된다. 예를 들어, n이 1,000,000일 때 약 1조 번의 연산이 필요하다.

에라토스테네스의 체 코드

function solution(n) {
  const primes = Array(n + 1).fill(true);
  primes[0] = primes[1] = false;
 
  for (let i = 2; i <= Math.sqrt(n); i++) {
    if (primes[i]) {
      for (let j = i * i; j <= n; j += i) {
        primes[j] = false;
      }
    }
  }
 
  return primes.filter((p) => p).length;
}

위 코드는 에라토스테네스의 체를 사용하여 소수를 판별한다.

primes 배열을 생성하여 0부터 n까지의 모든 수를 소수로 초기화한다.
0과 1은 소수가 아니므로 false로 설정한다.
2부터 √n까지 반복하면서, 현재 수가 소수인 경우 그 수의 배수를 모두 false로 설정한다.
마지막으로 primes 배열에서 true인 값의 개수를 세어 소수의 개수를 반환한다.

시간 복잡도 분석

반복문 1: i = 2부터 √n → 약 O(√n)
반복문 2: j = i * i 부터 n까지 → 전체적으로 O(n log log n) 정도
즉, 거의 선형에 가까운 매우 효율적인 소수 판별 알고리즘이다.